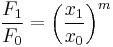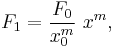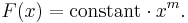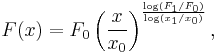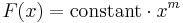Log-log plot
In science and engineering, a log-log graph or log-log plot is a two-dimensional graph of numerical data that uses logarithmic scales on both the horizontal and vertical axes. Because of the nonlinear scaling of the axes, a function of the form 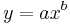 will appear as a straight line on a log-log graph, in which b will be the slope of the line (gradient) and a will be the y value corresponding to x = 1.[1]
will appear as a straight line on a log-log graph, in which b will be the slope of the line (gradient) and a will be the y value corresponding to x = 1.[1]
Contents |
Equations
The equation for a line on a log-log scale would be:
where m is the slope and b is the intercept point on the log plot.
Slope of a log-log plot
To find the slope of the plot, two points are selected on the x-axis, say x1 and x2. Using the above equation:
and
The slope m is found taking the difference:
where F1 is shorthand for F ( x1 ) and the same for F2. The figure at right illustrates the formula. Notice that the slope in the example of the figure is negative. The formula also provides a negative slope, as can be seen from the following property of the logarithm:
Finding the function from the log-log plot
The above procedure now is reversed to find the form of the function F(x) using its (assumed) known log-log plot. To find the function F, pick some fixed point (x0, F0), where F0 is shorthand for F(x0), somewhere on the straight line in the above graph, and further some other arbitrary point (x1, F1) on the same graph. Then from the slope formula above:
which leads to
Notice that 10log10(F1) = F1. Therefore, the logs can be inverted to find:
or
which means that
In other words, F is proportional to x to the power of the slope of the straight line of its log-log graph. Specifically, a straight line on a log-log plot containing points (F0, x0) and (F1, x1) will have the function:
Of course, the inverse is true too: any function of the form
will have a straight line as its log-log graph representation, where the slope of the line is m.
Applications
These graphs are useful when the parameters a and b need to be estimated from numerical data, and can also be used to estimate the fractal dimension of a naturally occurring fractal. Notably, when a probability distribution follows a power law, it will appear as a line on a log-log scale. These graphs are also extremely useful when data are gathered by varying the control variable along an exponential fashion. In this case, log-log graphing will yield a graph that shows the data points as evenly spaced, despite the compression of points at the low end.
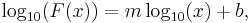
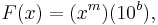
![\log[F (x_1)] = m \log (x_1) %2B b, \,](/2012-wikipedia_en_all_nopic_01_2012/I/6ca9cb42adaa9c803bc18f0953c35607.png)
![\mathrm {log}[F (x_2)] = m \log (x_2) %2B b. \,](/2012-wikipedia_en_all_nopic_01_2012/I/2dd3c8ba7a42e2a61f8ee72f10d5fe7e.png)
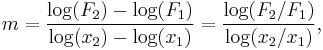
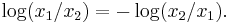
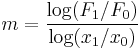
![\log(F_1 / F_0) = m \log(x_1 / x_0) = \log[(x_1 / x_0)^m ]. \,](/2012-wikipedia_en_all_nopic_01_2012/I/c5ee92fdbe2350f64be7fc0915a9ffae.png)